Category: GeoGebra Tutorials

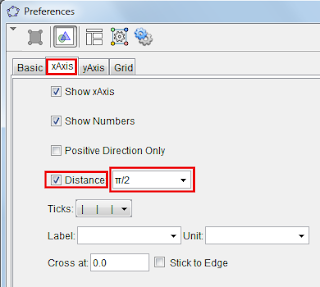
GeoGebra Tutorial: Exporting GeoGebra Worksheet to HTML 5

GeoGebra Tutorials
GeoGebra worksheets cannot run on devices that do not support Java. Examples of such devices are Apple’s iPads. To address this limitation, GeoGebra has created an export feature to HTML5. In this tutorial, we learn how to export a GeoGebra worksheet to HTML5.
Steps in Exporting a GeoGebra Worsheet to HTML5

1. Open the GeoGebra worksheet that you want to export to HTML5.   
2. Click the Filemenu, select Export, and then select Dynamic Worksheet as Webpage (html).


2. In the Dynamic Worksheet dialog box, select Export as Webpage button.
3. Type the Title of the web page and the texts needed above and below the construction.
4. Select the Advancedtab and be sure to check the Export to HTML only and Remove Line Breaks check boxes
5. Select File: html in the File section
6. Click the Exportbutton

The exported HTML file can be used as a web page or embedded to websites or blogs. The HTML5 page does not need Java in order to run. 
Leave a comment

GeoGebra Tutorial: How to change the x-interval to pi or pi/2

GeoGebra Tutorials
In graphing Trigonometric Functions, there are cases that you need to change the interval of the x-axis in terms of π.  In this tutorial, you will learn how to change the interval of the x-axis. 


1.) Right click a blank space on the Graphics view and then click on Graphics… from the pop-up menu to display the Preferences dialog box.


2.) In the Preferences dialog box, click on the xAxis tab, and then check the Distance check box.

.

3.) In the drop-down list box at the right of the Distance check box, select π or π/2 and then click the Close button to close the dialog box.

After step 3, the interval of the x-axis should be π or π/2.

Leave a comment

GeoGebra Tutorial: Constructing a Cardioid

GeoGebra Tutorials
A cardioid is a curve formed by moving circles. One of the ways to form a cardioid is shown below. In the applet (move the slider to the extreme right), the cardioid is given as the envelope of circles whose centers lie on a given circle and which pass through a fixed point on the given circle. 

Step by Step Instruction in Constructing the Applet Above

1. Construct point A at (0,0) and point B at (0,1).
2. Construct a circle with center A and passing through B. 
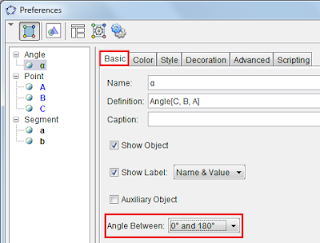
3. Construct an angle slider and set the minimum number to 0°, maximum number to 360° degrees and increment of 2°.  
4. Construct angle BAB‘. To do this, select the Angle with Given Size tool, click on point B and click on point A to display the Angle with Given Size dialog box. 
5. In the Angle with Given Size dialog box, replace 45° with α,  choose counterclockwise button, and then click OK. 
6. Hide the green sector by right clicking it and then clicking on the Show Object from the pop up menu.
7. Now construct a circle with center B‘ and passing through B.
8. Right click the circle with center B and  click Trace on. 
9. Move the slider and observe what happens. 
Leave a comment

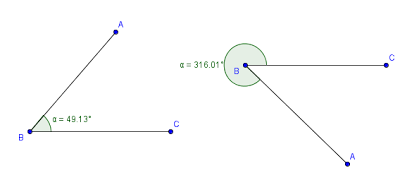
GeoGebra Tutorial: How to Disable Reflex Angles

GeoGebra Tutorials

In GeoGebra, we use the Angle tool to reveal angle measures.  By default, an angle can measure  up to 360°; however, there are instances that we want it to be less than or equal to 180°.  For example, we need to limit the angle measures of the interior angles of a polygon to 180° if we want to find its angle sum. 





In this tutorial, we learn how to disable angles measuring more than 180° but less than 360°.  Such angles are called reflex angles.  To disable reflex angles, do the following:

1. Right click the angle measure (green sector) and click Object Properties to display the Preferences window.


2. In the Preferenceswindow, click the Basic tab.
3. Select 0° and 180° in the Angle Between dialog box and then close the window. 

Leave a comment

GeoGebra Tutorial: Using the Perpendicular Line and the Point on Object Tools

GeoGebra Tutorials
In this tutorial, we use GeoGebra to explore the minimum sum of the distances of a point on the interior of a triangle to its sides. We learn how to use the Point on Object tool and the Perpendicular Line tool. We also learn how to compute using the Input bar. The final output of this tutorial is shown in the following applet.
This is a Java Applet created using GeoGebra from www.geogebra.org – it looks like you don’t have Java installed, please go to www.java.com
Steps in Creating the Applet


No
Instruction
1
Using the Polygon tool, construct triangle ABC. 
2
Select the Point on Object tool, and then click the interior of the triangle to create point D. 
3
move.pngMove point D and observe what happens. Can you move point D outside the triangle? 
4
Next, we create a line perpendicular to AB passing through D.  To do this, select the Perpendicular Line tool, select segment AB, and then select point D. 
5
Create two more lines passing through D, one perpendicular to AC and the other perpendicular to BC. 
6
intersect.png
Using the Intersect Two Objects tool, intersect the lines and the perpendicular segments. Your drawing should look like the figure below. 
7
Hide the three lines by right clicking each line and clicking them and selecting Show Objects. 
8
segment.pngUsing the Segment between Two Points tool, construct segments DE, DG, and DF. 
9
To find the total distance t of points D from E, F, and G, type t = g + h + i, and then press the ENTER key. 
10
move.pngMove the points to explore and observe the value of t. 



Application

A building is going to be constructed with a triangle bounded by the roads connecting Buildings A, B, and C. A connecting pathway is to be constructed from the three roads to the building. Find the location of the building that will minimize the cost of pathway construction.

Leave a comment

How to Embed An Applet in a Blogspot Post

GeoGebra Tutorials
Starting October 2012, the GeoGebra Institute of Metro Manila (GIMM) will be accepting post contributions from GeoGebra users in the Philippines. To those who are interested to share their applets, the tutorial below provides step by step instructions on how to upload applets in Blogspot, the platform used by GIMM. If you are interested to join, please email upnismedmultimedia@gmail.com 

Embedding an Applet in a Blogspot Post


1.) Open the GeoGebra worksheet that you want to embed in a Blogspot post. 

2.) Export the GeoGebra worksheet as HTML. This will display the exported worksheet as an applet in a web browser.

3.) In the web browser where the GeoGebra applet is displayed, right click a blank space outside the applet and the select View Source or View Page Source. This will display the HTML source code of the applet in another window or tab.


4.) In the source code window, copy the applet code; that is, copy the text from <applet> to </applet>



5.) Open the Blogspot post where the applet is to be inserted, and then select the HTML button to display its HTML view.

6.)  Paste the applet code on a location that you want it to appear 

7.) Select the Compose button to go back to the text view or click the Preview button to view how the applet will look like.

8.) Click the Save button.  

Leave a comment

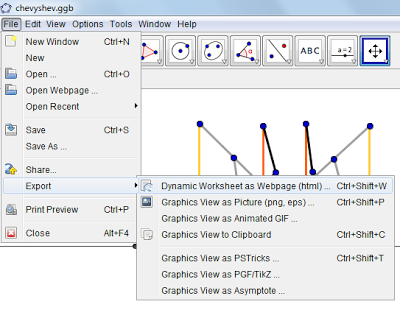
Tutorial 6 – Exporting Worksheet as HTML

GeoGebra Tutorials
It is possible to export a GeoGebra worksheet as an HTML web page. HTML webpages can be uploaded in websites as a stand alone page. 

To explort w Worksheet as a Dynamic HTML, do the following:

1.) Open the GeoGebra file that you want to export as HTML.
2.) Select the File menu, click Export, and then click Dynamic Worksheet as Web Page(html).  



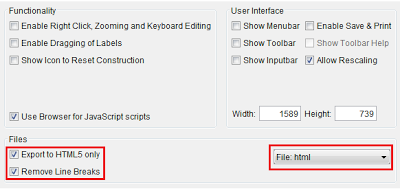
3.) In the Dynamic Worksheet Export dialog box, select Export as Webpage tab. 

4.) In the Export as Webpage tab, type the title of your worksheet in the Title text box, and then click Export when done.  This will open the Save dialog box.

5.) In the Save dialog box, type the name of your file and then click the Save button.

Saving the file will automatically open the HTML on your browser. 


Leave a comment

Free, Semi-free, and Dependent Objects

GeoGebra Tutorials
In GeoGebra, an object may be free, semi-free, or dependent. It is important to understand the differences among the three to perform effective geometric constructions.

This is a Java Applet created using GeoGebra from www.geogebra.org – it looks like you don’t have Java installed, please go to www.java.com

A free object does not depend on any object. You can move a free object anywhere on the Graphics view. In the figure above, points O and C are free objects. Point O determines the center of the circle which can be placed anywhere, and point C determines its radius.
A semi-free object, on the other hand, depends on one object. Semi-free objects can be moved but with restrictions. In the applet above, point A is a semi-free object. It can move, but only along the circumference of the circle.
Lastly, a dependent object depends on two or more objects. Unlike the other types of objects mentioned above, it cannot be moved by the mouse. For instance, point B above depends on point A and point C. Since it is the midpoint of points A and C, it will only move if point A or point C are moved. 
Exercise: In the applet Exploring Triangles, identify the free, semi-free, and dependent objects.

Snapshot

Leave a comment

Tutorial 5 – Graphs and Sliders

GeoGebra Tutorials

Objective: To explore the effects of a and b in the graph f(x) = a sin(x) + b.

No Tools Instructions
1
Open GeoGebra and use the View menu to display the coordinate axes.
2 slider.png Select the Slider tool and click on the Graphics view to display the Slider dialog box.
3
In the slider dialog box, select Number from the option buttons, and leave the other options as is. GeoGebra will automatically givea as the slider name.

slider-dialog-box.png
4
Now create slider b similar to slider a.
5
Type f(x) = a*sin (x) + b in the input bar and press the ENTER key to graph it.
6
Move the small circles on both sliders. What do you observe?

< Previous Tutorial

Leave a comment

Tutorial 4 – Graph, Text, and Latex

GeoGebra Tutorials
Objective: To construct graphs of linear and quadratic functions.
Tools: Insert Text

graph.png




No Tool Instructions
1
Open GeoGebra. Use the View menu to display the coordinate axes.
2
Type y = – x + 4 to construct a line passing through A and B.
3
Type f(x) = 0.5x^2 – 4.5x + 9 to construct a parabola passing through points A and B.
4
To construct the intersection, type A = (2,2) and B = (5,-1) in the input bar and press the ENTER key after each equation.
5 text.png We label the graphs. To label the graph of the quadratic function, click the Insert Text tool, and click on the Graphics view near the graph of the quadratic function to display the Text dialog box.
6
In the text dialog box, type f(x) = 0.5x^2 – 4.5x + 9 in the Edit text box, then click the Latex formula check box to check it, and then click the OK button. Notice what happens to the text.
7
Now, label the graph of the linear function and the coordinates of A and B with (2,2) and (5,-1) respectively.

< Previous Tutorial ** Next Tutorial >

Leave a comment
1 2