Approximating Pi
Move slider n to the right and observe what happens to the inscribed polygon.
The applet above shows the relationship between the area of a circle and the inscribed polygon. Notice that as the the number of sides (n) of the inscribed polygon increases, its area gets closer and closer to the area of the circle which is equal to 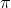 . This approximation is called the method of exhaustion. It was developed used by Archimedes.
. This approximation is called the method of exhaustion. It was developed used by Archimedes.