Task 4 – Point of Similarity
Questions
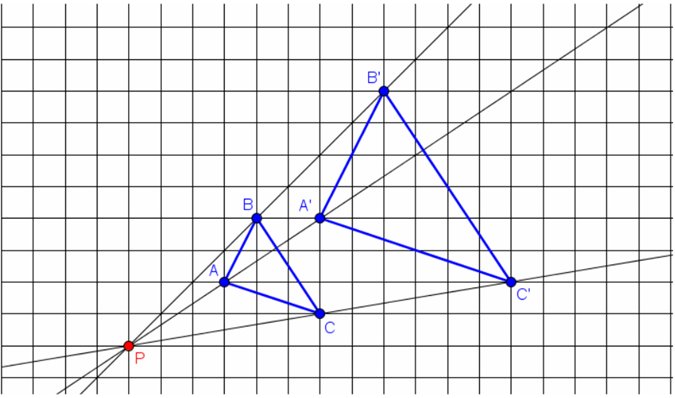
1.) Are the two triangles similar? Why?
2.) What is the ratio of the lengths of their corresponding sides?
3.) Use the Line tool to connect the corresponding vertices of the two triangles. Did your observations in Task 2 and Task 3 hold?
4.) Make a conjecture about the lines connecting the corresponding vertices of similar triangles.
[toggle title=’Explanation’ title_font_size=’14px’]If two triangles are similar and their corresponding sides are parallel, then the line connecting their corresponding vertices will intersect at a point. This point is called the center of similarity or point of similarity.
In Task 3, $latex \triangle ABC \sim \triangle A’B’C’$ and their corresponding sides are parallel. The three lines connecting the corresponding vertices intersect point $latex P$ as shown above. In Task 4, $latex \triangle STU \sim \triangle MNO$, but their corresponding sides are not parallel, so the three lines connecting their corresponding vertices do not intersect at a point.
[/toggle]
Task 5 >>