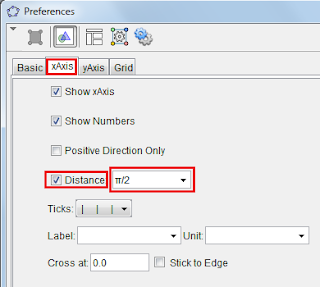
Five Squares to One
Move points A and B to resize the squares. Drag the slider to the extreme right to move the parts of the square.
Snapshot

Snapshot

Reference:
“Five-Squares-to-One Dissection” from the Wolfram Demonstrations Project
http://demonstrations.wolfram.com/FiveSquaresToOneDissection/
“Five-Squares-to-One Dissection” from the Wolfram Demonstrations Project
http://demonstrations.wolfram.com/FiveSquaresToOneDissection/
Contributed by: Izidor Hafner